Distributed Training Made Easy with PyTorch-Ignite
Writing agnostic distributed code that supports different platforms, hardware configurations (GPUs, TPUs) and communication frameworks is tedious. In this blog, we will discuss how PyTorch-Ignite solves this problem with minimal code change.
Crossposted from https://labs.quansight.org/blog/2021/06/distributed-made-easy-with-ignite/
Prerequisites
This blog assumes you have some knowledge about:
-
PyTorch’s distributed package, the backends and collective functions it provides. In this blog, we will focus on distributed data parallel code.
-
PyTorch-Ignite. Refer to this blog for a quick high-level overview.
Introduction
PyTorch-Ignite’s
ignite.distributed (idist) submodule introduced in version
v0.4.0 (July 2020) quickly turns single-process code into its data distributed version.
Thus, you will now be able to run the same version of the code across all supported backends seamlessly:
-
backends from native torch distributed configuration: nccl, gloo, mpi.
-
Horovod framework with
glooorncclcommunication backend. -
XLA on TPUs via pytorch/xla.
In this blog post we will compare PyTorch-Ignite’s API with torch native’s distributed code and highlight the differences and ease of use of the former. We will also show how Ignite’s auto_* methods automatically make your code compatible with the aforementioned distributed backends so that you only have to bring your own model, optimizer and data loader objects.
Code snippets, as well as commands for running all the scripts, are provided in a separate repository.
Then we will also cover several ways of spawning processes via torch native torch.multiprocessing.spawn and also via multiple distributed launchers in order to highlight how Pytorch-Ignite’s idist can handle it without any changes to the code, in particular:
More information on launchers experiments can be found here.
PyTorch-Ignite Unified Distributed API
We need to write different code for different distributed backends. This can be tedious especially if you would like to run your code on different hardware configurations. Pytorch-Ignite’s idist will do all the work for you, owing to the high-level helper methods.
Focus on the helper auto_* methods
This method adapts the logic for non-distributed and available distributed configurations. Here are the equivalent code snippets for distributed model instantiation:
| PyTorch-Ignite | PyTorch DDP |
|---|

| Horovod | Torch XLA |
|---|

Additionally, it is also compatible with NVIDIA/apex
model, optimizer = amp.initialize(model, optimizer, opt_level=opt_level)
model = idist.auto_model(model)
and Torch native AMP
model = idist.auto_model(model)
with autocast():
y_pred = model(x)
This method adapts the optimizer logic for non-distributed and available distributed configurations seamlessly. Here are the equivalent code snippets for distributed optimizer instantiation:
| PyTorch-Ignite | PyTorch DDP |
|---|

| Horovod | Torch XLA |
|---|

This method adapts the data loading logic for non-distributed and available distributed configurations seamlessly on target devices.
Additionally, auto_dataloader() automatically scales the batch size according to the distributed configuration context resulting in a general way of loading sample batches on multiple devices.
Here are the equivalent code snippets for the distributed data loading step:
| PyTorch-Ignite | PyTorch DDP |
|---|
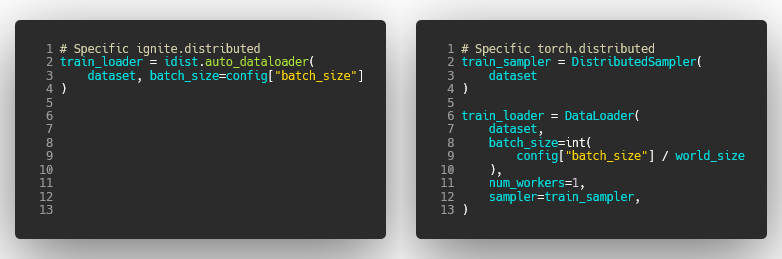
| Horovod | Torch XLA |
|---|

NOTE
Additionally, idist provides collective operations like all_reduce, all_gather, and broadcast that can be used with all supported distributed frameworks. Please, see our documentation for more details.
Examples
The code snippets below highlight the API’s specificities of each of the distributed backends on the same use case as compared to the idist API. PyTorch native code is available for DDP, Horovod, and for XLA/TPU devices.
PyTorch-Ignite’s unified code snippet can be run with the standard PyTorch backends like gloo and nccl and also with Horovod and XLA for TPU devices. Note that the code is less verbose, however, the user still has full control of the training loop.
The following examples are introductory. For a more robust, production-grade example that uses PyTorch-Ignite, refer here.
The complete source code of these experiments can be found here.
PyTorch-Ignite - Torch native Distributed Data Parallel - Horovod - XLA/TPUs
| PyTorch-Ignite | PyTorch DDP |
|---|---|
| Source Code | Source Code |
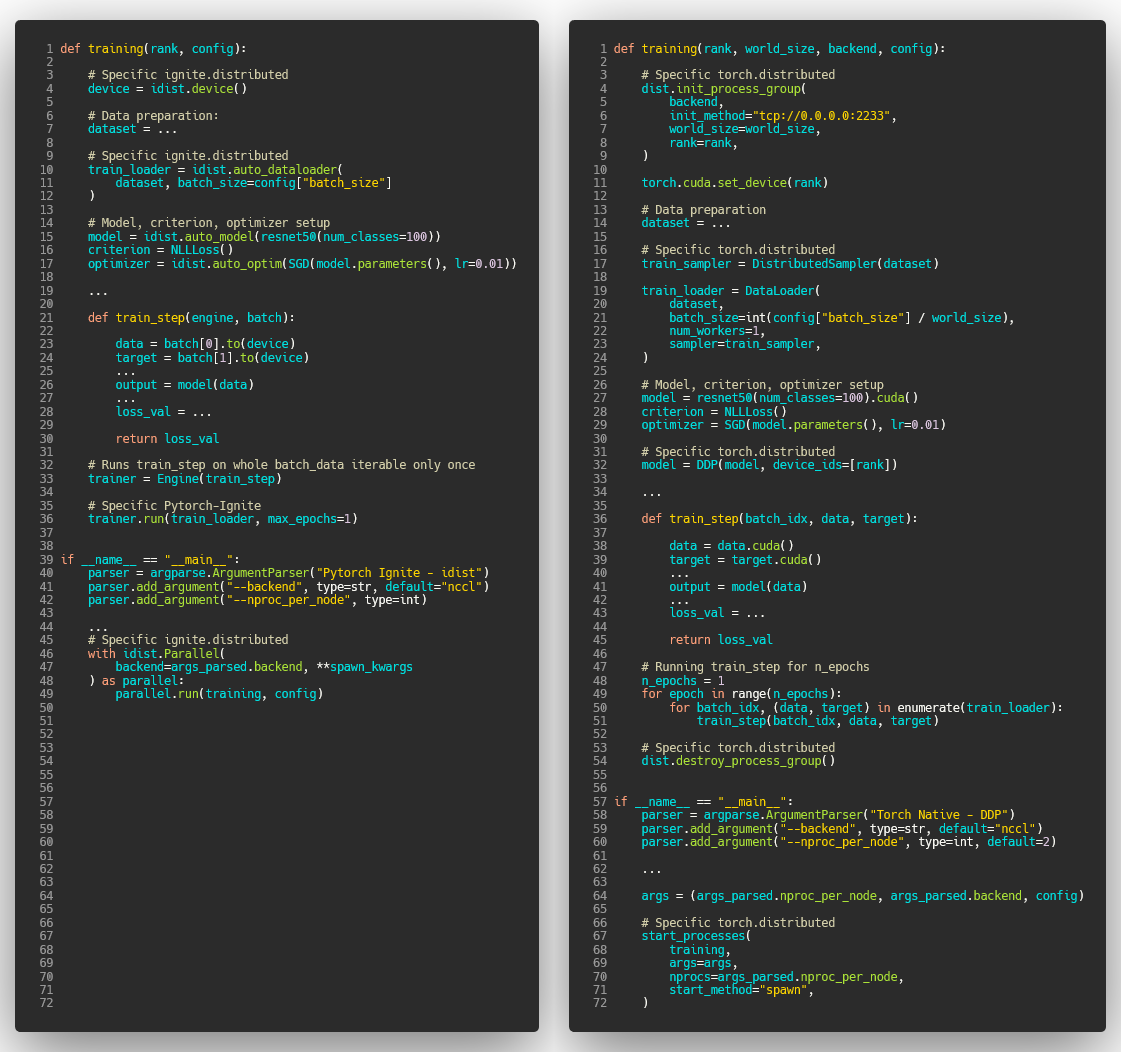
| Horovod | Torch XLA |
|---|---|
| Source Code | Source Code |
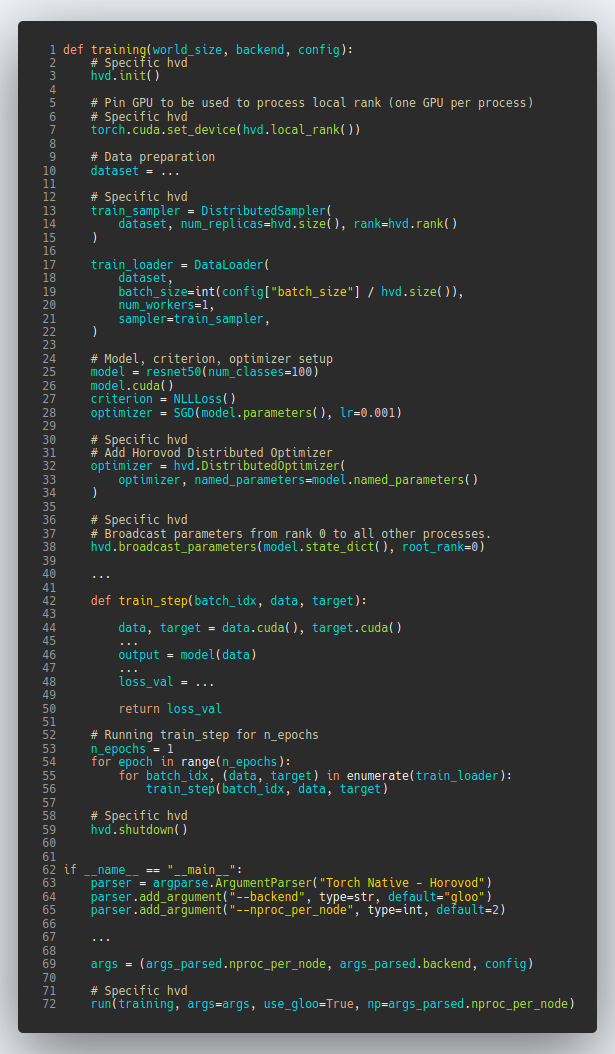
|
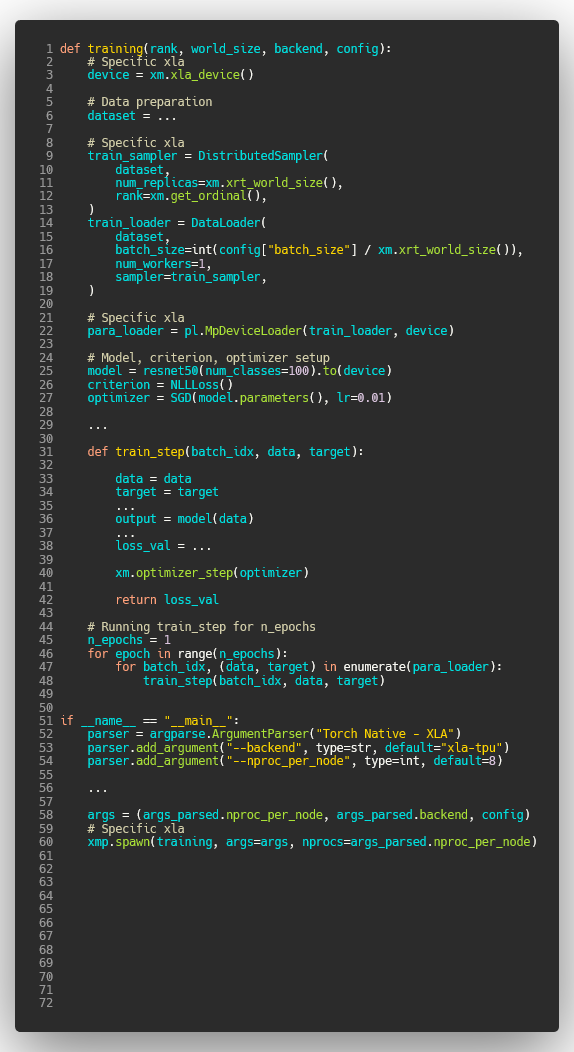
|
NOTE
You can also mix the usage of idist with other distributed APIs as below:
dist.init_process_group(backend, store=..., world_size=world_size, rank=rank)
rank = idist.get_rank()
ws = idist.get_world_size()
model = idist.auto_model(model)
dist.destroy_process_group()
Running Distributed Code
PyTorch-Ignite’s idist also unifies the distributed codes launching method and makes the distributed configuration setup easier with the
ignite.distributed.launcher.Parallel (idist Parallel) context manager.
This context manager has the capability to either spawn nproc_per_node (passed as a script argument) child processes and initialize a processing group according to the provided backend or use tools like torchrun, slurm, horovodrun by initializing the processing group given the backend argument only
in a general way.
With torch.multiprocessing.spawn
In this case idist Parallel is using the native torch torch.multiprocessing.spawn method under the hood in order to run
the distributed configuration. Here nproc_per_node is passed as a spawn argument.
- Running multiple distributed configurations with one code. Source: ignite_idist.py:
# Running with gloo
python -u ignite_idist.py --nproc_per_node 2 --backend gloo
# Running with nccl
python -u ignite_idist.py --nproc_per_node 2 --backend nccl
# Running with horovod with gloo controller ( gloo or nccl support )
python -u ignite_idist.py --backend horovod --nproc_per_node 2
# Running on xla/tpu
python -u ignite_idist.py --backend xla-tpu --nproc_per_node 8 --batch_size 32
With Distributed launchers
PyTorch-Ignite’s idist Parallel context manager is also compatible
with multiple distributed launchers.
With torchrun
Here we are using the torchrun script in order to
spawn the processes:
torchrun --nproc_per_node 2 ignite_idist.py --backend gloo
With horovodrun
horovodrun -np 4 -H hostname1:2,hostname2:2 python ignite_idist.py --backend horovod
NOTE
In order to run this example and to avoid the installation procedure, you can pull one of PyTorch-Ignite’s docker image with pre-installed Horovod. It will include Horovod with gloo controller and nccl support.
docker run --gpus all -it -v $PWD:/project pytorchignite/hvd-vision:latest /bin/bash
cd project
With slurm
The same result can be achieved by using slurm without any
modification to the code:
srun --nodes=2
--ntasks-per-node=2
--job-name=pytorch-ignite
--time=00:01:00
--partition=gpgpu
--gres=gpu:2
--mem=10G
python ignite_idist.py --backend nccl
or using sbatch script.bash with the script file script.bash:
#!/bin/bash
#SBATCH --job-name=pytorch-ignite
#SBATCH --output=slurm_%j.out
#SBATCH --nodes=2
#SBATCH --ntasks-per-node=2
#SBATCH --time=00:01:00
#SBATCH --partition=gpgpu
#SBATCH --gres=gpu:2
#SBATCH --mem=10G
srun python ignite_idist.py --backend nccl
Closing Remarks
As we saw through the above examples, managing multiple configurations and specifications for distributed computing has never been easier. In just a few lines we can parallelize and execute code wherever it is while maintaining control and simplicity.
References
-
idist-snippets: complete code used in this post.
-
why-ignite: examples with distributed data parallel: native pytorch, pytorch-ignite, slurm.
-
CIFAR10 example of distributed training on CIFAR10 with muliple configurations: 1 or multiple GPUs, multiple nodes and GPUs, TPUs.